 |
Math Cats for Teachers and Parents |
 Math Cats for Kids |
|
| * lots of activities for beginning multiplication
> I am going to introduce multiplication; any advice on how --
Use oodles of manipulatives. Use them over and over and over
again. It is impossible to do too much work with math
manipulatives when you are introducing multiplication! Here
are some inexpensive ideas (as well as ideas for
manipulatives that cost $$). All of them reinforce the idea
that multiplication is repeated addition.
1) Egg carton math. Have each child bring in an egg carton
and a plastic container with some type of little objects.
These could be pennies, beads, buttons, paper clips, raw
macaroni, mini-pompoms... whatever. When you say and write a
problem, such as 3 x 4, the children need to display this
problem using different sections of the egg carton to hold
each group.
By the way, I always told my students to think of the X in a
multiplication problem as meaning "groups of." So 3 x 4
is "3 groups of 4."
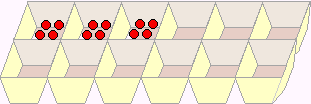 Using the egg carton, then, they would only use 3 compartments, and they would put 4 items in each of those 3 compartments, counting as they go. And also after the problem is set up, they can count by those 4's: 4, 8, 12.
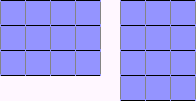
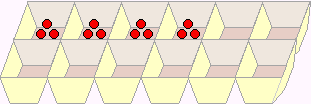 Then you could say, "4 x 3." Now they need 4 groups of 3, so they'll use 4 compartments and put 3 items in each, but they will still have 12. Count by those 3's: 3, 6, 9, 12. 2) Turn multiplication problems into rectangles. The cheapest way is just to use graph paper and color in squares. So again, with 3 x 4 (3 groups of 4), to show 3 groups of 4, students would color 3 rows with 4 squares in each row (4 + 4 + 4). To show 4 x 3 (4 groups of 3), students would color 4 rows with 3 squares in each row. They can then compare these two rectangles and see that in both cases, 12 squares are colored, but one looks like the other, turned 90 degrees.
 The more expensive but more effective way to make rectangles is with Cuisenaire rods. This way the colors also help to reinforce the problems. To show 3 x 4, you'd need 3 purple (4) rods. To show 4 x 3, you'd need 4 light green (3) rods. I wanted so badly for my students to each have a set of "Cuisenaire rods" to use at home that we made our own 2D version. I just made photocopies of centimeter grid paper onto stiff card stock. Then the students colored portions of the grid paper with crayons, using the 10 colors needed to match the rods and then cut them out with scissors. So, for instance, red rods are the length of two units (the white rods). So if they needed 10 red rods, they would need to color 20 squares red, then cut them out in clumps of two. They would need 30 light-green squares to make 10 light- green "three" rods. And so on. If you don't actually have the rods, the colors are:
Anyhow, the students colored and cut up all these strips and put them in an envelope with a clasp (actually, a ziploc bag would be better) for taking back and forth between home and school. The next thing I did was to make a multiplication table for each child, also using centimeter graph paper. It had the numbers 1 - 10 running down the left side and running across the top, with a multiplication sign in the top left corner. Then there was a thicker line to separate out the answers. (Or you could write those numbers 1 - 10 in a different color from the answers. But it still helps to have a thicker line.) Either I or the students would fill in the answers, but it is essential that they are accurate. You can do this in stages. So while you are just working with the twos times table, just give them a grid where those facts are filled in. Gradually fill in more of the grid. Now, let's pretend they are working on their 3's so we can use the same example as above. The grid is filled in with all of the 1's, 2's, and 3's running across as well as down: 3, 6, 9, 12, 15, 18... If you ask them to show 3 x 4, they will think: Okay, 3 groups of 4, so I need 3 of my purples. They will lay these down on the multiplication grid, starting at the top left corner of the answer area. Then they will peek under the bottom right corner of their rectangle. They should find a 12 there. Now if you ask them, 4 x 3, they will think, Okay, 4 groups of 3, so I'll need 4 light-greens. They will lay these down in the same way and peek under the bottom right corner. Again they should find a 12. I'm going to try to insert a few graphics here: first the grid (this one shows all the answers to 10x10):
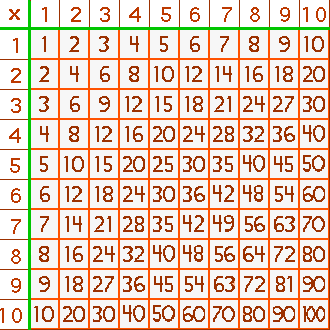 And now the two problems showing 3 x 4 and 4 x 3 (with the grid numbers covered by the rods shown):
3) Lay Cuisenaire rods along a centimeter ruler, again to show multiplication as repeated addition. For 3 x 4, you would lay 3 purple rods end to end and see that they have reached 12 on the ruler. 4) Once the students become very good with the rods and multiplication grid, start turning the grid into a missing- number problem sheet. But scramble things up. Again use a partial grid while they are learning. But instead of writing the numbers in order across the top, write, for instance, 2, 5, 3, 1... and down the left side, 3, 1, 5, 2... and ask the students to fill in the answers. When they master that, sprinkle some answers around but take out some of the numbers from the outer edge, and the students need to figure out what number fits there. If they see a 15 on their grid, they will realize that the missing number at the top must be a 3 or a 5. If another number in that column is 6, then they know the number at the top must be a 3. As I continued to create these missing-number grids for my students, they got better and better at their logical reasoning as well as their facts, and I began to remove more and more numbers. I got it down so that eventually I could put 10 well-placed numbers in the answer part of the grid, and they could complete the rest of the puzzle... 110 missing answers (90 more from the answers and the 20 missing numbers from the top and left edges)! It was a real challenge for them, logically, while reinforcing the facts. In fact, you could ask your students to create some of these puzzle sheets. Simply creating them is another exercise in logic.
Enough!! I just want to say that we used manipulatives
throughout the year for multiplying. Drown them in
manipulatives!! I also want to say that I have turned some
of these activities into online activities at Math Cats (for
instance, a multiplication grid activity... where each
student originally had a magnetized set). I
Wendy P of Math Cats, on teachers.net math board | ||||||||||||||||||||||
| * How do you teach multiplication?
> Do you teach as a whole class (group) or teach individual
I like to start with the circles and stars approach found in
Math by All Means: Multiplication, Grade 3 [at amazon.com]
by Marilyn Burns. The hands on ideas/lessons in this book
are great.
Colleen:)/k-3, on teachers.net primary elementary board
- - - - -
Using a Number Line
I used to post a huge number line across the top of
the blackboard, with every 10 highlighted in yellow, and
I'd use a yardstick to point to the numbers while we'd skip-
count by a particular number. I wanted them to develop a
mental number line for multiplication, to visualize the facts
linearly. (It also helped them with their mental addition.)
Using Multiplication Grids
And then in terms of a 10 x 10 grid, we used to use magnetic
number squares on metal boards, and the students would race
to see how fast they could place all 100 products on the 10 x
10 board in the right locations. Inevitably some numbers got
lost or mixed with another student's set, so eventually I
developed the same game for computer. It is now online at
Math Cats, specifically:
http://www.mathcats.com/microworlds/multiplication_grid.html
You need to download a MicroWorlds plug-in to use the
project, but you can preview it (screenshot plus project
description) at
http://www.mathcats.com/microworlds/multiplicationgrid_overview.html
Wendy P of Math Cats
- - - - -
Sixes, Sevens and Eights
> I was wondering if someone could give me a better way of
We talk about sets, arrays, repeated addition, skip counting,
and the family of facts. We use counters, spinners, graph
paper, songs, and games. Relate the sixes to the threes, and
the eights to the fours.
Pat, on the teachers.net primary board
- - - - -
Multiplication is not repeated addition.
On your site you mention that you reinforce the idea that multiplication is repeated addition. Unfortunately, it isn't.
There are occasions where it seems like that, but it will give the students the wrong impression when they later
meet 5 * 0.316, for example. Adding 5 to itself 0.316 times?
Please see www.maa.org/devlin/devlin_06_08.html for further details.
Regards, | ||||||||||||||||||||||
| * Multiplication Songs
> I am starting to teach my children the times tables. I
People still teach the times tables? Be still my beating
heart, and I wish I could get your students. My eighth
graders have no idea how to multiply even simple numbers.
But, I digress. May I suggest one of my favorites from my
childhood that is now out on video. School House Rock ...
the multiplication rock video. Sure, they're corny, but they
might work. And, it's wonderful for me to watch (if we get
the chance that is) and reminisce.
You can purchase the [DVD] through amazon.com:
Schoolhouse Rock - Multiplication Classroom Edition [Interactive DVD]
John, on teachers.net math board
- - - - -
I came to your site looking for suggestions. I home school my son and flash cards were just SO boring. I felt stuck. As I read through some great suggestions, I checked out the School House Rock. I got the Anniversary edition with every song ever made. My son LOVES it, I can do leave him in front of the tv and he is learning his tables, grammar, science and America facts!!!
He got out of bed last night complaining he couldn't turn the math off in his head! I can't say enough how great this is!
Schools should use this and forget the state testing garbage. Teach the essentials! Of my three children, THIS one is going to know his multiplication tables WELL, he will know how to spell and he will have a good vocabulary--unlike my older children who are going through public school. I missed my opportunity with them, I regret this immensely.
Anyway, THANK YOU and to anyone else looking, this DVD set at $14.99 through Amazon is PRICELESS!!!!!!!!!!!
Diane Hall, message to Math Cats
- - - - -
Check out Hap Palmer's Multiplication Mountain CD at happalmer.com, featuring upbeat, original songs and a colorful activity guide designed to be used in the classroom or at home.
Hap is a pioneer in the area of movement and music in education. His inspiration for this new CD came from his own daughter's experience in learning multiplication in third grade. The "mountain" approach seems to be very effective.
Beth B., message to Math Cats
- - - - -
I found the book at school that has the
multiplication songs in it (and many other great ideas to teach
multiplication facts). The book is: Making Multiplication Easy:
Strategies for Mastering the Tables Through 10/ Grades 2 - 4. It's a Scholastic
book. The author is Meish Goldish.
LK, on the teachers.net main board
| ||||||||||||||||||||||
| * Multiplication Rhymes, Chants, and Stories
> I am looking for ideas to teach multiplication facts to 4th
Multiplication Rhymes and Stories
We make up silly sayings to remember the hard ones. The kids
really get in to making up ones for their hard ones. Ex:
"Had two 8's, dropped them on the floor, picked them up, had 64."
My third graders love to tell a new one they have thought up!
Jam, on teachers.net math board
- - - - -
I am teaching an undergraduate course, and several of the
participants want those rhymes
to help their students remember those troublesome facts. I
have the following, but would be interested in hearing
others, etc.
Multiplication Rhymes
4 x 4
6 x 6
7 x 7
8 x 8
4 x 6
7 x 4
4 x 8
6 x 7
7 x 8
6 x 8
KathyB/1st/IA, on the teachers.net math board
- - - - -
I have seen where students write their own rhymes to the
military march tune. Ex:
7 times 7 is 49, don't bend down you'll hurt your spine.
Think of the rhythm when soldiers are marching and have kids
work in groups to come up with them, then class votes on best
and can make a book of class best multiplication marches.
KAT, on teachers.net upper elementary board
- - - - -
Marching
Wendy P of Math Cats, on teachers.net upper elementary board
| ||||||||||||||||||||||
| * multiplication Web sites
> Do you have any great lesson plans or sites for teaching multiplication?
Michele's Math Multiplication Tips
Multiplication: An Adventure in Number Sense
http://www.multiplication.com
- - - - -
Check out Sum Fun at www.oswego.org/ocsd-web/games/SumSense/summulti.html.
You need to arrange the number cards to make a true multiplication number sentence. Set the clock for how many problems you think you can complete in 1 or 2 or ... minutes.
Wendy P. of Math Cats
- - - - -
Here is a listing of the other multiplication web sites and pages mentioned elsewhere on this page:
SchoolHouse Rock
Schoolhouse Rock lyrics and video links
another site for Schoolhouse Rock lyrics and video links
Multiplication Mountain at Hap Palmer's music site
- - - - -
Multiplication activities here at Math Cats:
Interactive Multiplication Table
(The next two interactive projects require downloading the MicroWorlds plug-in; the links below take you to descriptions and screenshots of the projects with links to the projects and the plug-in download page.)
Multiplication Rods
Multiplication Grid | ||||||||||||||||||||||
| * When do you teach multiplication?
> I am a first year third grade teacher who has to teach
When isn't as important as how!
There's no rush. But do make sure you teach understanding not just the rote skill.
Before you even introduce times tables, teach and re-teach the adding of groups. Then work your way up to the idea that multiplication is the short cut to adding groups (e.g. two groups of two is the same as 2 X 2. Teach students to read the "X" sign as "groups of").
You can even make a class book of different groups which can be added together (3 + 3 + 3 = 9) and also shown as multiplication (3 x 3 = 9). Students can illustrate the groups (3 groups of 3 cats) and then make their individual pages into a class book which then can be borrowed by a different student each night. Get parents to write comments in the back.
You could even do facts to 12 and have students work to make books for each group, i.e. adding groups of 1, groups of 2, etc.
Michael, on the teachers.net math board
p.s. If you teach multiplication this way, you'll find they understand division better when you teach it as dividing into groups.
- - - - -
In our curriculum, multiplication comes after graphing, building
large numbers, and computation including addition and
subtraction with lots of trading.
I do measurement and then time and then multiplication comes
during January.
If you can find the series of books by Marilyn
Burns you will get lots of hands on activities for multiplication
and division. And I take all the time until March Break with
multiplication.
Suzanne, on the teachers.net math board
- - - - -
I think that there are different reasons for teaching
multiplication at different times. None are wrong. At my
school, we start multiplication the first week of school (I teach
3rd also). The kids have had exposure to the basic concepts in
2nd grade and are excited about it. This also gives the kids who
struggle with understanding how it works and memorizing the facts
(do not forget to make sure that they understand) more time to
learn the facts before the end of the year (and the high stakes
testing). At the beginning of the year, we stick with 1 digit x
1 digit. At the end of the year (around March/April) we go back
to multiplication and do multi-digit multiplication. This way,
those kids who struggled have had time to work on the basics
before getting to the harder parts. We also integrate teaching
multiplication and division. We do a lot with the fact families--
it really helps. Our math books have multiplication/division in the
middle of the year (if we went in order, we would probably start
around Feb.-- but since I am about 2 weeks away from starting Chapter
1, you can see that we don't follow the order of the book all
that well!) All 5 third-grade teachers follow the same basic
concept order in math (for convenience mainly).
I would say to just pick when you think it best fits into your
plan. I would suggest not leaving it for last if you have
testing since it takes many kids some time for the concept to
sink in.
We do single-digit multiplication/division, then fractions/decimals, then
place value, then multi-digit addition/subtraction, then multi-digit multiplication. We fit in the statistics, geometry,
algebra, mathematical reasoning, and measurement wherever and
whenever we can throughout the year.
T, on the teachers.net math board
- - - - -
Yes, read books by Marilyn Burns
Read anything she has written. She offers some very good
activities, and, even better, she explains what results you can
expect. My textbook seems to introduce multiplication late in the
year, also. You can start some of her activities much earlier,
giving you a head start. For example, my students love the circle
and stars game and its follow-up discussions. They also liked
looking for various patterns in a hundreds chart. They should have
been introduced to the idea of multiplication last year, so don't
feel like you are starting too early. My friend and I will soon
have them copy those dreaded lists of facts. They will know that
the facts will eventually have to be memorized. Come spring, they
will start having times quizzes, which they love, stopwatch and
all. In theory, I love all the activities that help them understand
the concept of multiplication, but every year it comes down to
memorization.
susan, on the teachers.net math board
- - - - -
Kim, I also teach third grade. As I introduce multiplication,
I say, " 2 groups of 3" as I write 2 x 3. I do this for
several weeks. I then have my children draw 2 groups of 3.
etc. This third six weeks, we have started with the
multiplication facts on a much tougher level. The students
understand the concept of multiplication and we are just
working on learning the facts. We will really hit them after
Christmas though.
Vonda, on the teachers.net math board | ||||||||||||||||||||||
| * reteaching and reviewing multiplication
> I'm a 6th grade Resource teacher. I teach one Math class
You might try this: develop some pages with 100
multiplication facts on each one in no particular order.
Make several different pages with the same facts but mixed
up, and identify each different page with a letter to keep
track more easily. Don't forget to use the zero and one facts
too. Then use it like a contest, only each student competes
against himself. The goal is to complete the sheet in five
minutes or less with NO mistakes. Give each student a copy
of sheet A and set the class timer for 5 minutes. The
student tries one sheet a day (this makes good bell work,
too!) and each day tries to better his time and his
accuracy. When he's mastered sheet A (goal met 3 days in a
row), give him sheet B, then when he's mastered that give him
sheet C. You can make several versions, with the A page
using lots of zeroes and ones, and the last pages using more
10, 11, and 12 facts. By the time the student has mastered
all of the versions (five or six should do it -- if not, make
up page G, H, I, J, K, however many it takes), he's mastered
multiplication facts.
Try not to let them make it a competition among themselves,
because doing it better than somebody else is not the
important thing. Promote the idea of "personal best." Try
to get them to encourage each other to simply do their best.
You could provide a special reward of some sort (if you're
allowed to use edibles, one small hard candy or a tiny
tootsie roll works wonders! Here we have to give them an
"IOU" until after lunch) each time a student meets a daily
goal and moves on to the next sheet. (Getting 3 rewards in a row establishes an expectation.) Then do the same thing with
division facts, then move on to equivalent fractions [1/4 =
blank/8, blank/16 = 1/2, etc], and then to conversion of
fractions to decimals and decimals to fractions when you get
to that (you won't do a hundred of these on one page! Maybe
start with 40, then 50 and then 60 max)[ex: 1/2 =.5 = 50%;
1/4 = 25% = .25, 3/4 = 75% = .75, and so on with fifths,
sixths, eighths, tenths, and sixteenths - the most common
fractional parts used in daily living]
Sorry this is so long. Let me know how this goes! Good luck!
Linda, on teachers.net math board
- - - - -
> HELP! 6th graders can't mult and div need help:
You can't teach them anything past 2 digit multiplication and
division unless you go back and teach it. I teach 5th grade and
I spend a LONG period of time teaching multiplication and
division. They need a lot of practice with these concepts to
learn them. If your math book doesn't teach it, you're going
to have to use your own resources. You need to start small and
build up the concept. Go back to 2 digit x 1 digit. You
also will need to spend time on it if they're going to learn
it. Your administration may not like it, but they'll not be
able to learn anything more advanced without the basics. I don't
really know of any fun games.
You can use place value blocks with place value boards to teach the concept with manipulatives, first, but other than that, I use pencil/paper.
Also, try to incorporate as many real-world problems that will also make
sure they master the concept and not just the rote skill of
multiplying/dividing.
jody, on teachers.net upper elementary board
- - - - -
You need to cipher daily
What is cipher, you may ask? Ask your grandmother. She did
it, and she probably still know how to multiply and divide.
It is just a game. Choose up sides any way you like. (I do it
randomly the first time, then put winners at the top next
time. We start the game at the bottom.) Start at the bottom
of the 2 lists. Students have a best of three contest, in
which the loser gets to choose the type of problem, ie add,
subtract, multiply, divide, fractions, etc. I make up the
problems as we go along and work them at the same time as the
students. I also require all students at their desks to work
the problems.
I do this 15 minutes per day, and the game is
ongoing. When the game is over, we start a new one. There are
several different versions of this game, but I can tell you
that by the time my students get out of my class in May, they
are so much more advanced than any of their peers in the
other classes, that it isn't even funny. BUT, it takes a
commitment of 15 minutes per day.
Phil, on teachers.net multiplication board | ||||||||||||||||||||||
| * 2-digit multiplication
> I need to teach 2-digit multiplication to a third grade
Please don't rush to teach 2-digit multiplication
From everything I know about third grade math, it is not
appropriate to be teaching two-digit multiplication yet.
Usually that would be done in grade 4, or at the end of grade
3 if the students are extremely solid with one-digit
multiplication. From my experience, it takes months and
months of hands-on work with one-digit multiplication facts
for students to be really solid with the concepts
(multiplication as repeated addition, etc.) as well as being
really solid with the facts. Rushing into two-digit
multiplication can backfire on you. You can end up with
students who learn the steps for doing things without
really "getting it."
If you are a student teacher, I am assuming that you have
been instructed by your master teacher to introduce this
material, so you may not be able to control the timing... but
you can try. Have the students done lots and lots of hands-
on work with one-digit multiplication and do they know all of
those facts cold? If not, what is the rush? If you have
been working with hands-on materials, then you can extend
them for two-digit work if you absolutely must proceed with
this lesson.
I highly recommend Cuisenaire rods for
introducing even two-digit multiplication work. You could
also use Base Ten Blocks. To do 2-digit work with Cuisenaire rods:
Say you are multiplying 23 x 4. Well, I always tell my
students to think of the "x" as "groups of," so this would be
23 groups of 4. However, it is much easier to examine 4
groups of 23. (Do your students know, from lots of earlier
work, that a x b = b x a ? I hope so!!! If not, you are
wasting your time to be doing 2-digit work.) Anyhow, the
orange rods = 10, so you could set out 4 groups, each of
which has 2 orange rods and 1 light green (3) rod. Then you
can see that you have 8 orange rods (80) and 4 light green
rods (4 x 3) or another 12, and 80 + 12 = 92.
If you did the same problem with Base Ten Blocks, you'd still
have 8 orange rods and you'd have 12 single white cubes,
still illustrating that you've got 80 + 12.
Now if you need to move right away into the algorithm (again,
I hope you don't have to rush it), you could first break the
problem up into expanded notation: 20 x 4 + 3 x 4 = 80
+ 12 = 92.
I did a lot of this, breaking the problem up
into two smaller problems, with my third-graders at the end
of the year. A lot of them still struggle with multiples of
10. (They know that 2 x 4 = 8 but sometimes get stumped on
20 x 4. That is why they need to SEE it in rods, and count
it up (repeated addition.))
After you do lots and lots of that expanded notation work,
finally you can show them that the standard algorithm
multiplies the ones digits first (4 x 3). You could show
them about writing the two below the line and carrying the
one above the 2 (the tens place in 23), but many people
prefer another stage first, where you write the whole 12
below the line, then multiply 4 x 2 , which is really 4 x 20,
and write 80 below the 12, and add them to get 92.
But anyhow, you just asked about introducing 2-digit
multiplication, so I certainly hope you are not going to get
into the standard algorithm for many weeks.
You also asked about relating multiplication to division.
Again, this should be done extensively with single-digit work
before ever considering getting into the 2-digit
relationships. When you do hands-on work, the relationship
is obvious. In my earlier post, I talked, for instance,
about placing little objects into the sections of egg
cartons. If you show 3 x 4 by placing four items into each
of 3 sections (3 groups of 4), you see that you have 12 in
all, and you also see that 12 divided into 3 groups gives you
4 in each group. And so on. The relationship between
multiplication and division can (and probably should) be
illustrated with virtually every hands-on problem every day.
Don't even THINK about doing two-digit division in November
of third grade, OK???
Wendy P of Math Cats, on teachers.net math board |
|
|
| © copyright Wendy Petti of Math Cats. All Rights Reserved. |